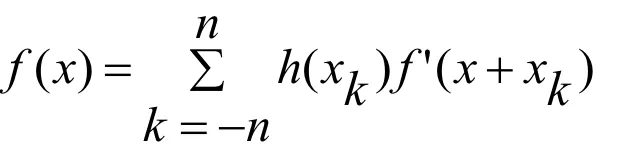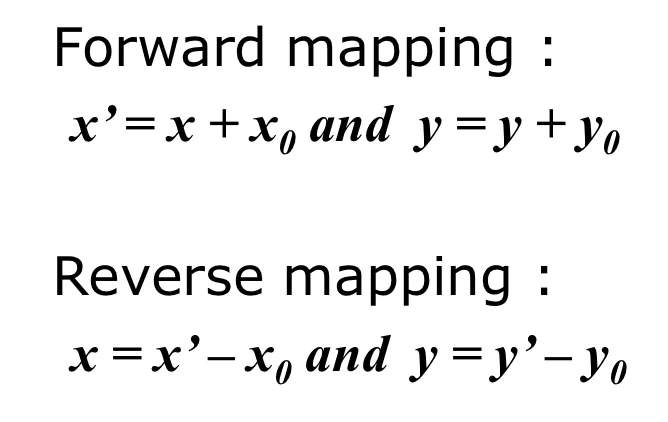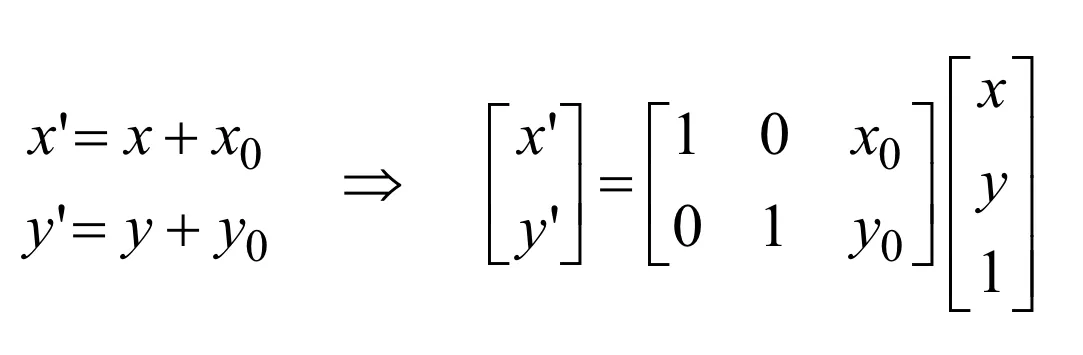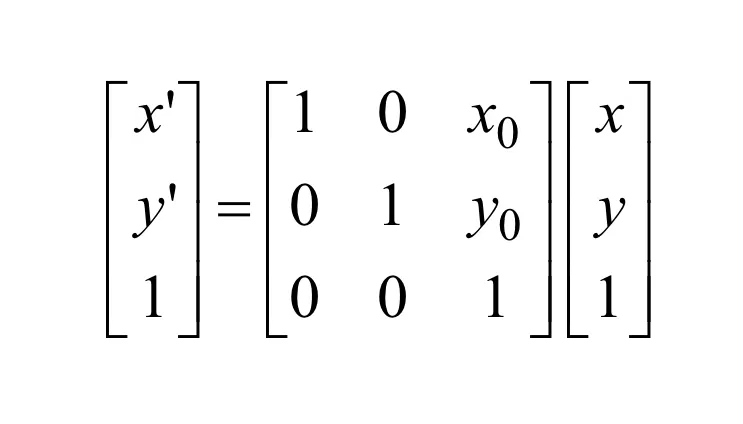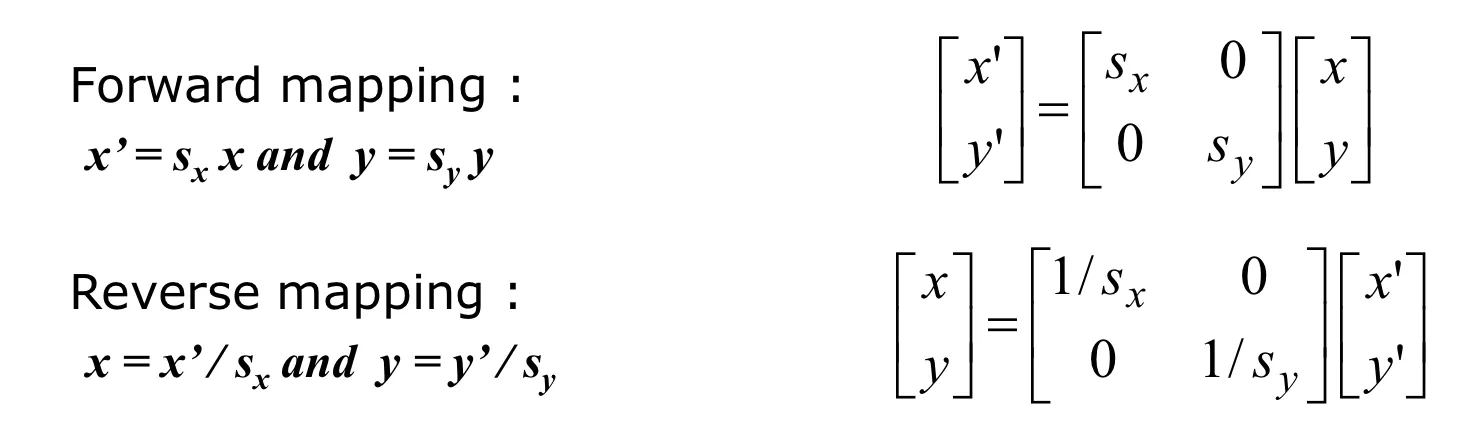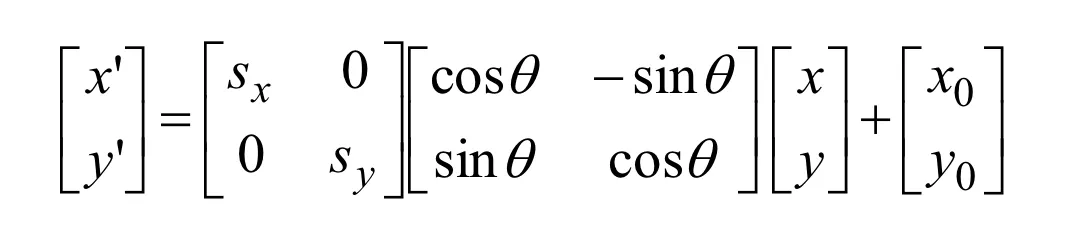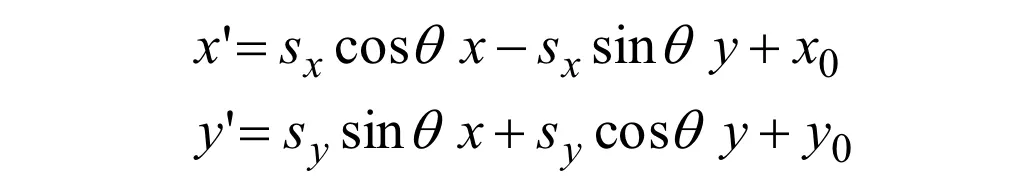Search
✅

4. Geometric Process

링크
Category
Keywords
상위 개념
하위 개념
속성
Subcategory
날짜
•
change the position or arrangement of the pixel. Not change the value
•
Interpolation
•
linear
◦
translation
◦
rotation
◦
scaling
•
non-linear
◦
warping
◦
pincushion
◦
barrel
◦
keystone
◦
skew

Forward mapping

I(x,y)→O(x‘,y‘)I(x, y) → O(x^`, y^`)
간단하게 input pixel 과 output pixel을 사상하는 것. 함수와 같음.
문제점 : Holes, Overlaps → 사이즈를 조정하다보면 빈공간이나 겹치는 부분이 생길 수 있음.

Reverse / Inverse mapping

I(x‘,y‘)←O(x,y)I(x^`, y^`) ← O(x, y)
Forward의 반대. Forward의 문제점을 해결. 역함수가 필요하다.

Interpolation

Mapping의 문제점은 Subpixel이 발생할 수 있다는 것이다.
ex) func(x,y) → (x/2, y/2) : 값이 1이면 subpixel 문제 발생
이는 Interpolation 함수를 이용해서 해결 가능.
h(x):interpolationFunc/Kernelf’(x):inputf(x):interpolatedoutputh(x) : interpolation Func / Kernel\\f^’(x) : input\\f(x) : interpolated output
여기서 사용되는 interpolation kernel에는 여러 종류가 있다.
•
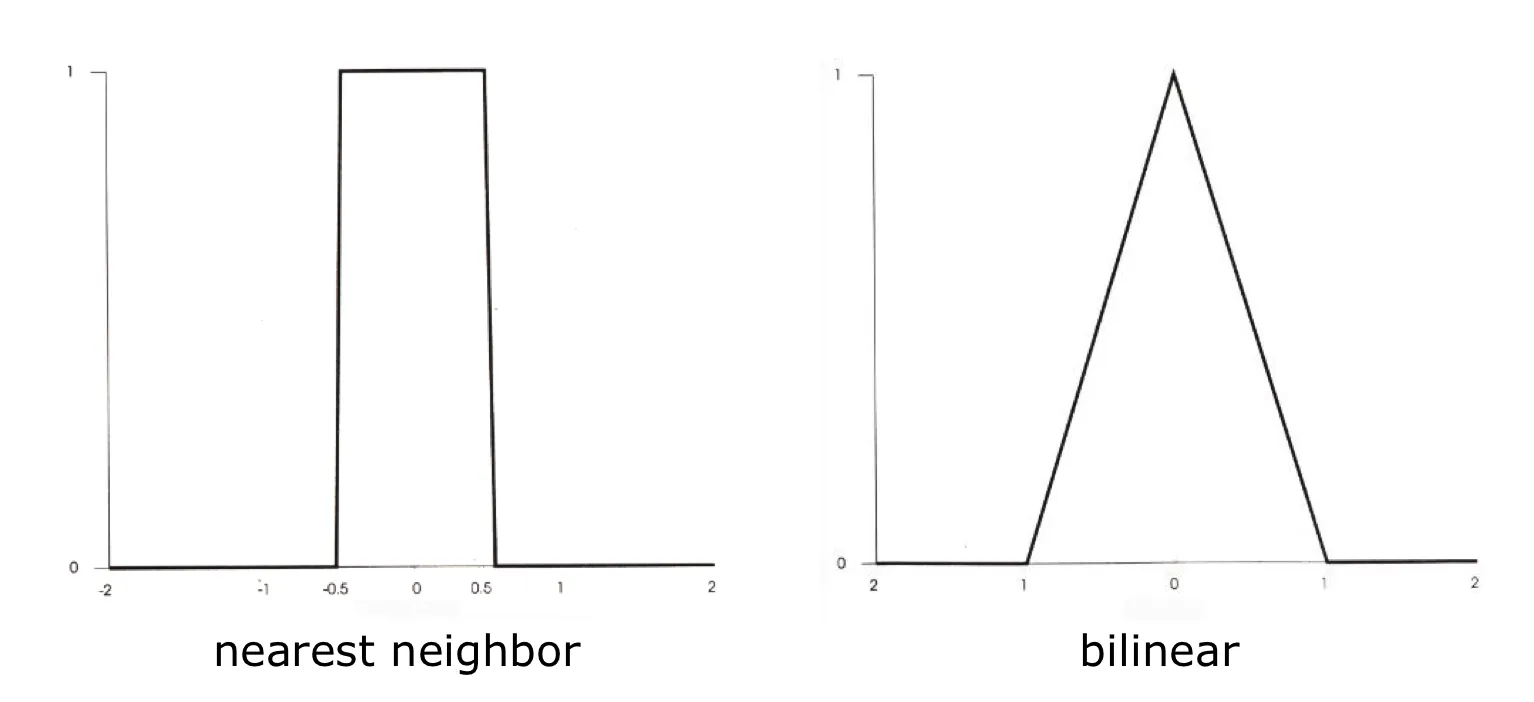
Nearest Neighbor interpolation kernel : 최근접 화소 보간 커널
•
bilinear interpolation kernel : 양선형 보간 커널
•
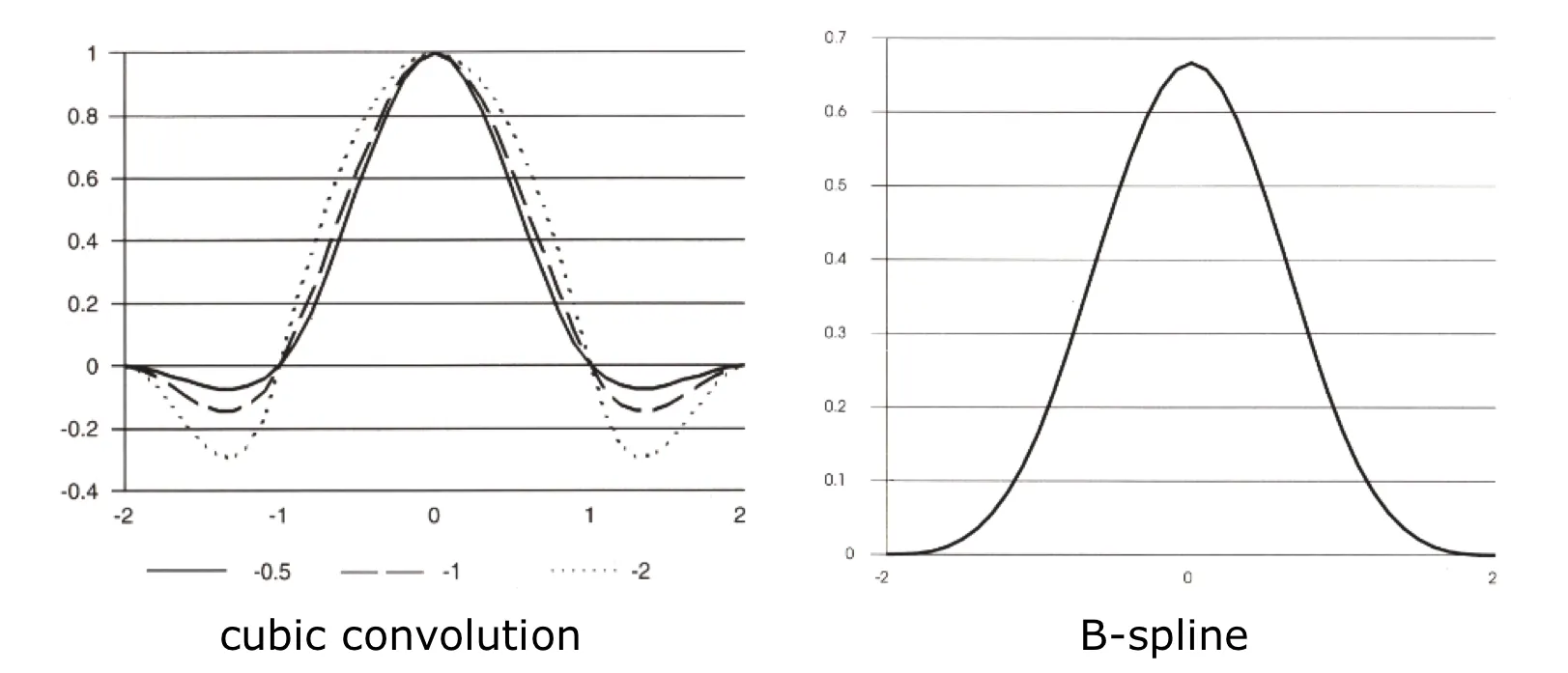
cubic conv IK : 3차 회선
•
B-spline IK : B-스플라인
0.5는 0이다

특징

•
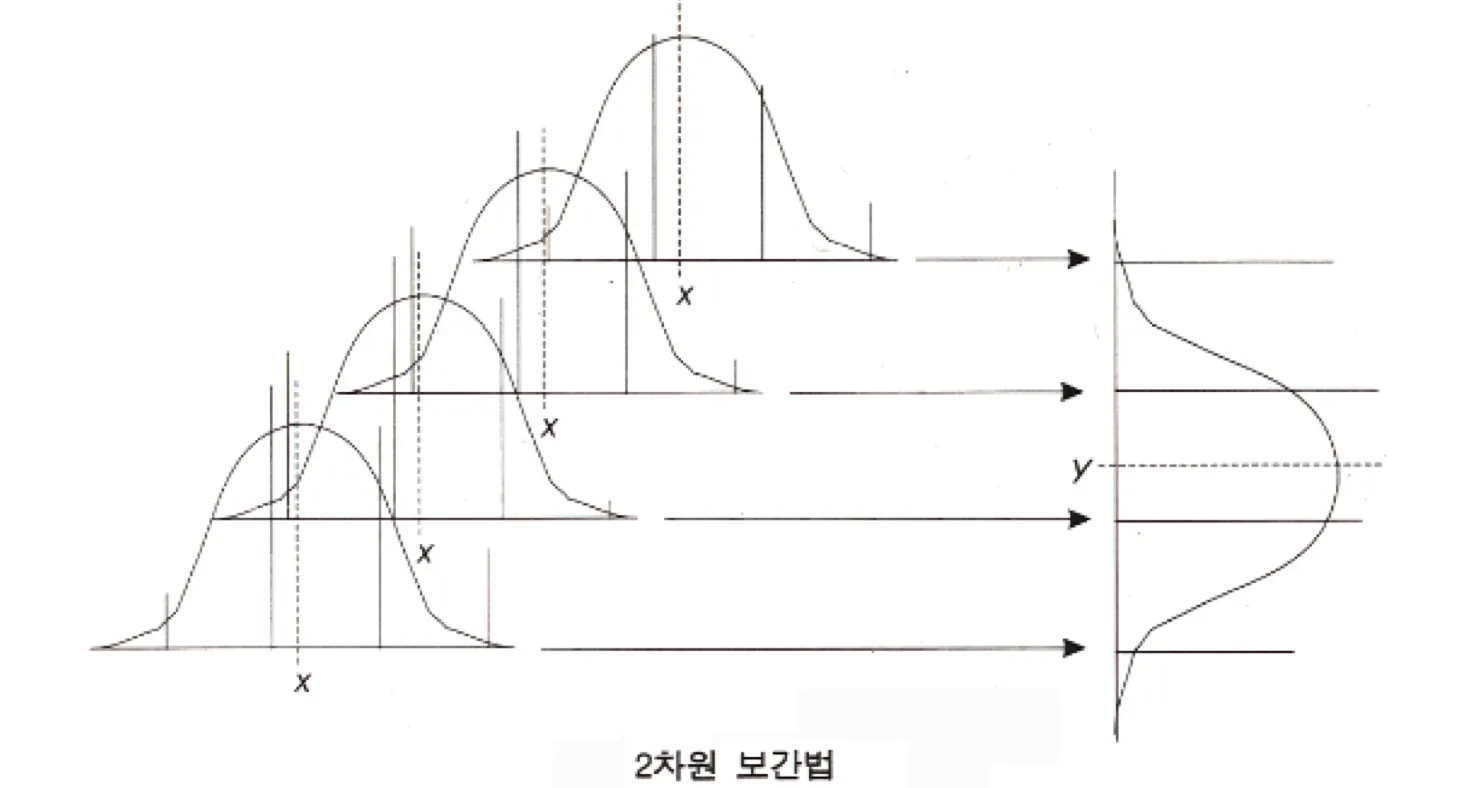
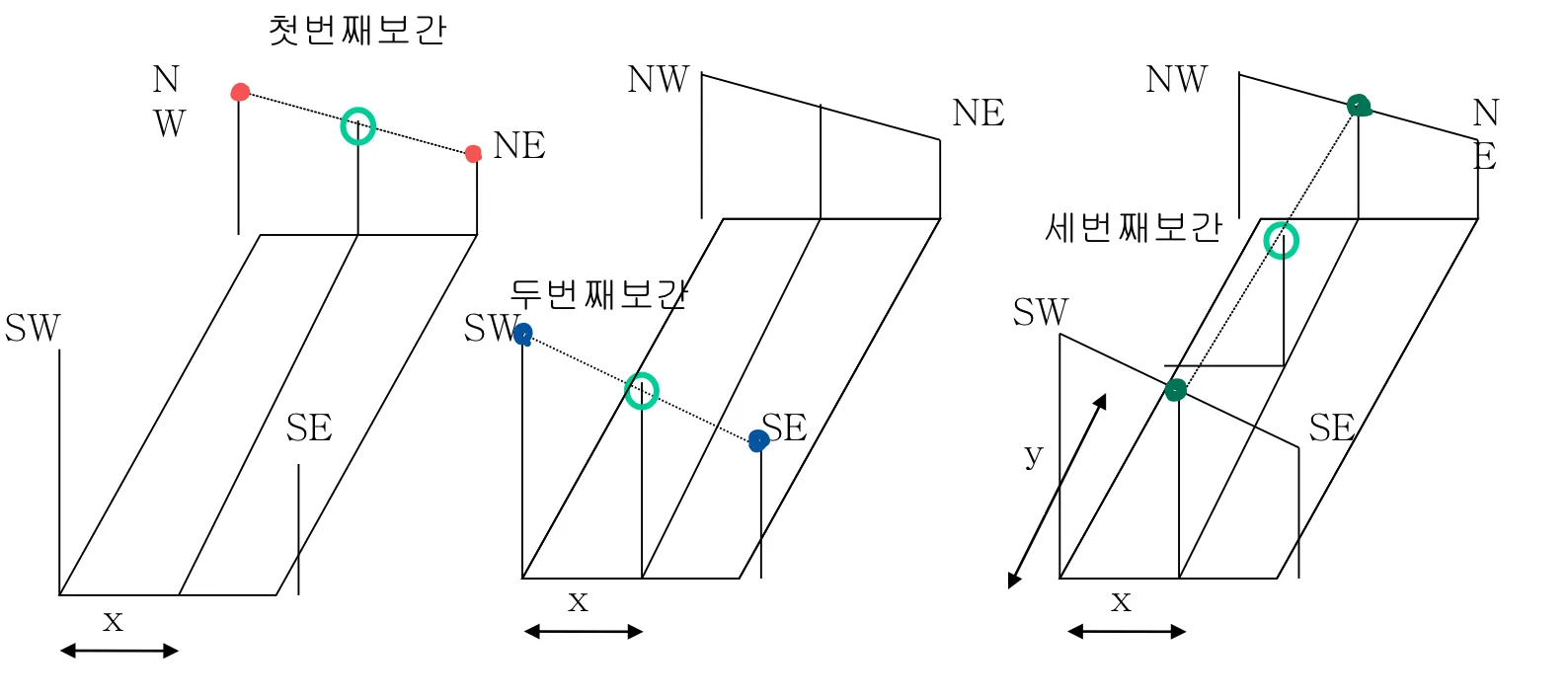
Separability : 2D 이미지를 1D로 한줄 씩 나눠서 연산을 한다. row 값들을 보간하고 해당 값들에 대해 다시 보간(col)
•
Cubic convolution
f(x)={(a+2)∣x∣3−(a+3)∣x∣2+10<= |x|<1a∣x∣3−5a∣x∣2+8a∣x∣−4a1<=|x|<202<=|x|f(x) = \begin{cases} (a+2)|x|^3 - (a+3)|x|^2 + 1 & \text{0<= |x|<1}\\ a|x|^3 - 5a|x|^2+8a|x|-4a & \text{1<=|x|<2}\\0 & \text{2<=|x|} \end{cases}
•
B-spline
f(x)={1/2∣x∣3−∣x∣2+2/30<= |x|<1−1/6∣x∣3+∣x∣2−2∣x∣+4/31<=|x|<202<=|x|f(x) = \begin{cases} 1/2|x|^3-|x|^2+2/3 & \text{0<= |x|<1}\\ -1/6|x|^3+|x|^2-2|x|+4/3 & \text{1<=|x|<2}\\0 & \text{2<=|x|} \end{cases}

Translation

이미지 이동시키는 기법. 보간법과 마찬가지로 Forward, Reverse 방법이 있다.
여기서 더해고 빼지는 값이 정수가 아니라면 Interpolation이 필요하다. [Subpixel 문제]
정방행렬
이를 행렬로 표현하면 위와 같다.

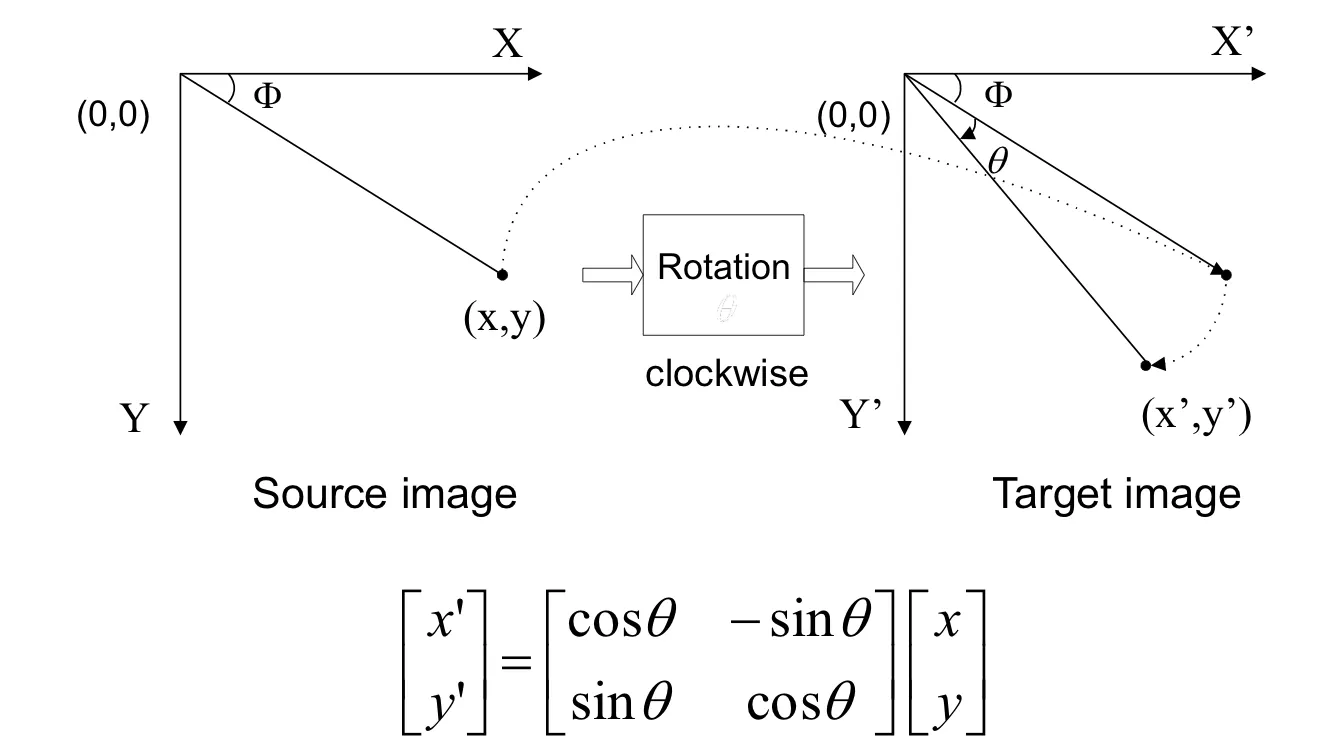
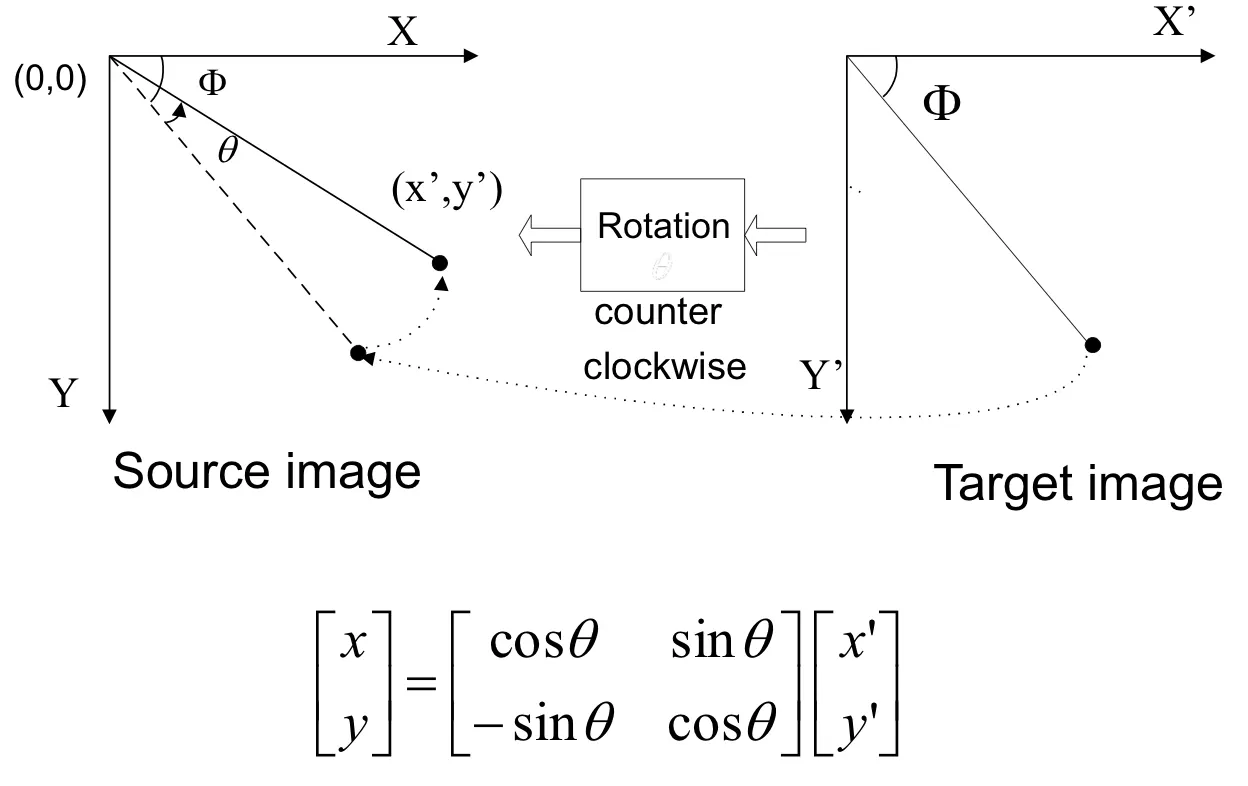
Rotation

이미지 회전시키는 기법.
•
Forward mapping : 이미지 중심에 대해서 rotation하려면 x, y대신 x - center, y - center 값을 넣어야함
•
Reverse mapping :

Scaling

이미지의 사이즈를 조정한다.
•
Size Up
◦
magnification, scaling up, zooming, up-sampling, stretching, enlargement
•
Size Down
◦
minification, scaling down, decimation, down-sampling, shrinking
•
특징
◦
기본 해상도에서 더 높일 수는 없다
◦
Down sampling 후에는 Low pass가 필요하다. 사이즈 줄이는 게 고려할 게 많다.

Mirroring

Flip.

Composition

Translation, Rotation, Scaling을 한번에 나타내면 다음과 같다.