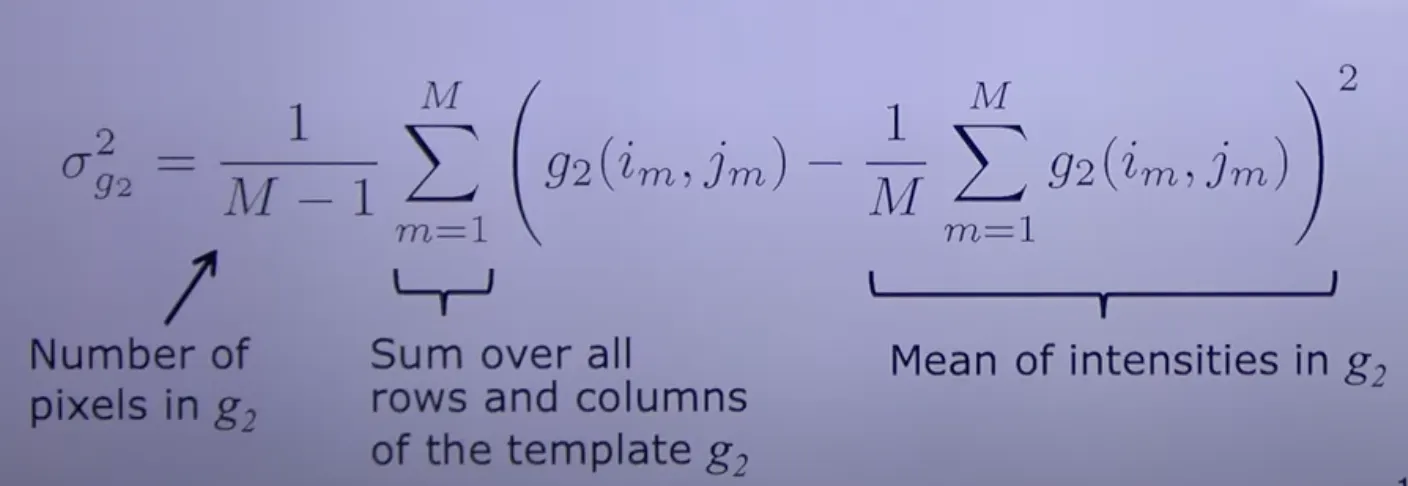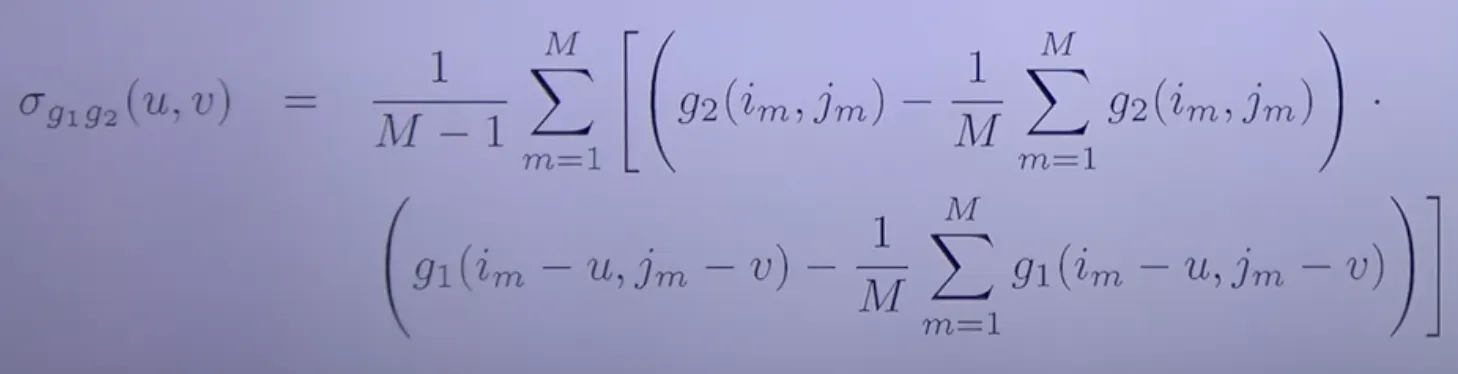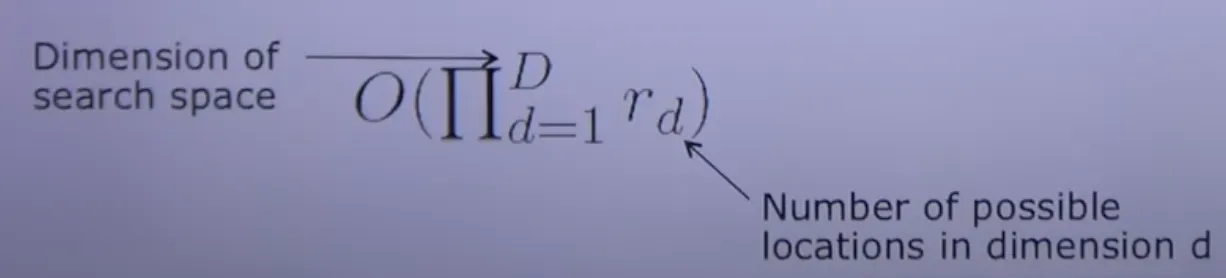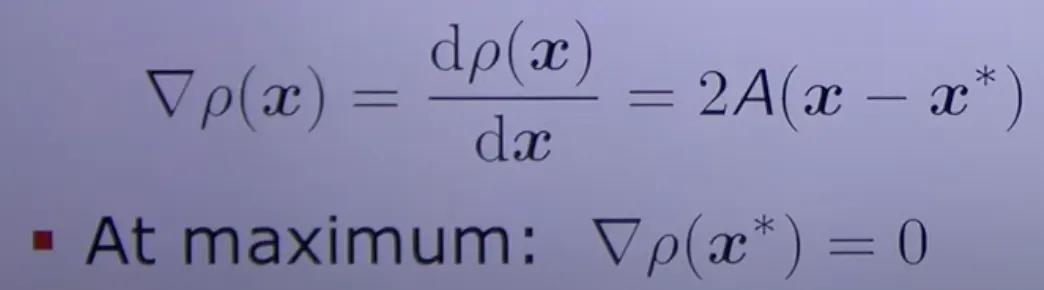Cross Correlation
•
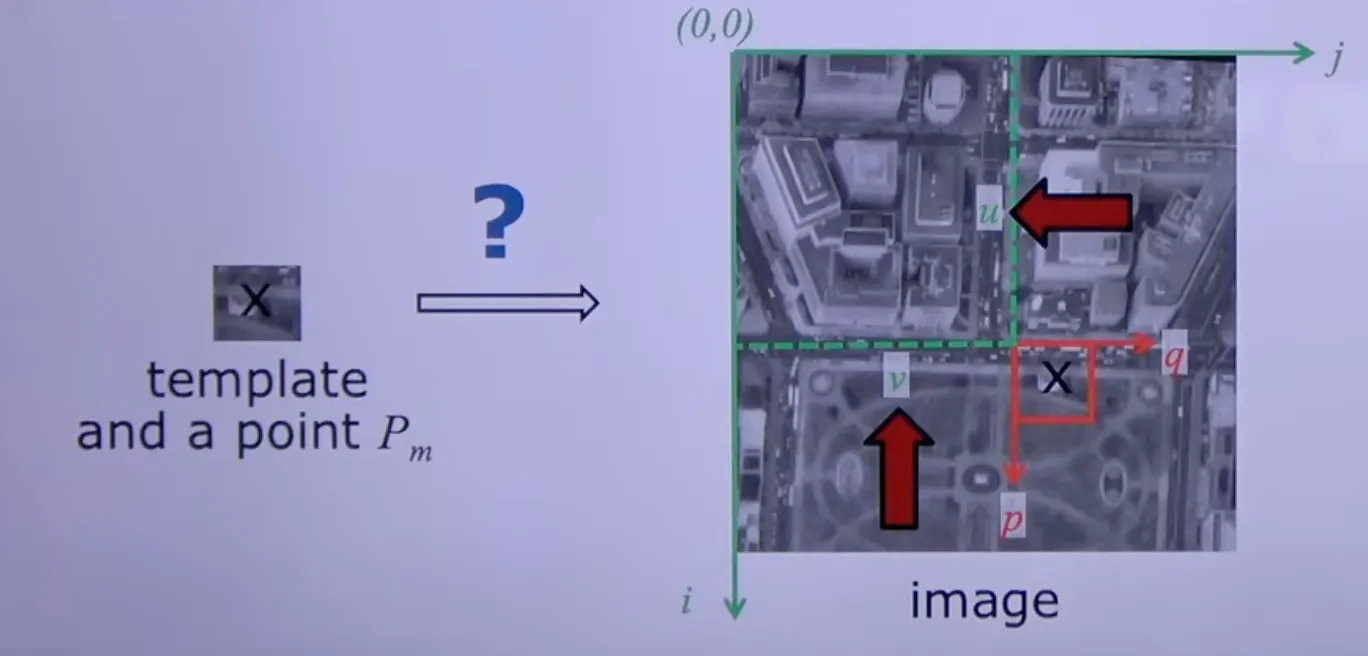
Find certain image content in an image
•
determine its location in the image
•
Key assumption : images differ only by
◦
translation
◦
brightness
◦
contrast
여기에 rotation은 끼지 못함. → 왜?
하나의 템플릿이 이미지 상에 어디있는지 알려면 여러 가지 offset 필요
I, j 축이 있으면 template의 좌상단을 기준으로 (u,v)를 알아야함.
2222
T_G는 translation
T_I의
•
a : brightness - 평균치를 높이는 역할을 하는데 이는 밝기를 높이는 것과 연결
•
b : contrast 변수
목적은 이 값들을 구해서 Maximize similarity을 위함
Similarity를 비교하는 방법
Cross Correlation Function
σ : standard deviation : 표준편차
[u,v]를 추정하는 방법은 모든 가능한 위치에서의 Cross Correlation 계수를 최대치로 하는 곳을 찾는 거지
σ_g1(u,v) : 템플릿 크기(u,v)만큼 원본 이미지에서 subimage로 변환해서 템플릿이랑 비교하기 위함
NCC
•
g1, g2 Variance
M의 크기는 템플릿의 크기. (i_m - u, j_m - v)는 해당 사이즈만큼의 부분만 확인하기 위함
Complexity
scale, shear, rotation parameter등 여러 차원의 parameter가 추가된다면 complexity가 급격히 증가하게됨
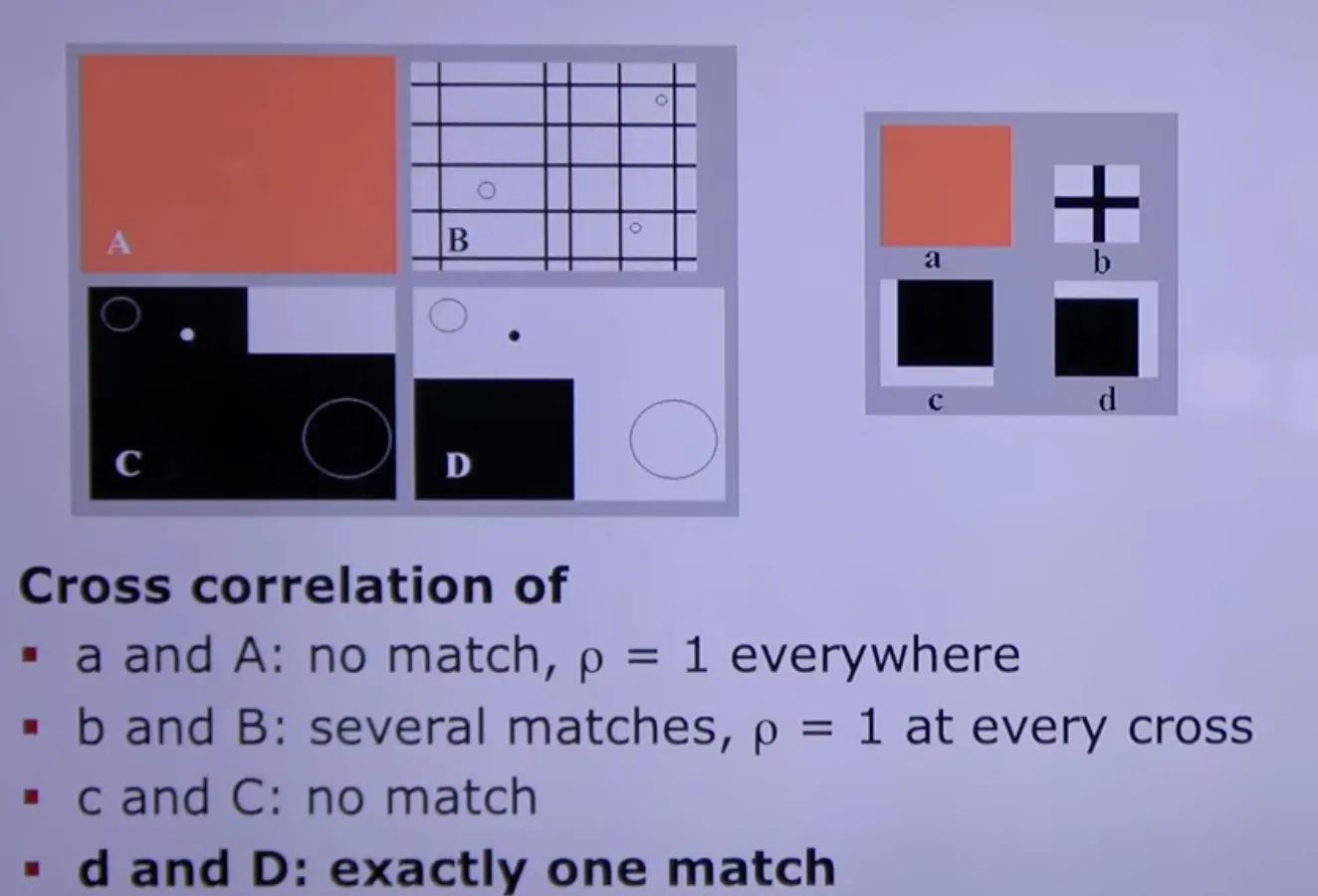
Example
Basic CC 정리
•
하나의 이미지에서 template image를 찾는 방법론
•
translation, brightness, contrast의 변수에 대해 성립가능
•
brightness, contrast는 CC function 안에서 변할 수 있다.
•
search space는 translation parameter에 의해 변한다
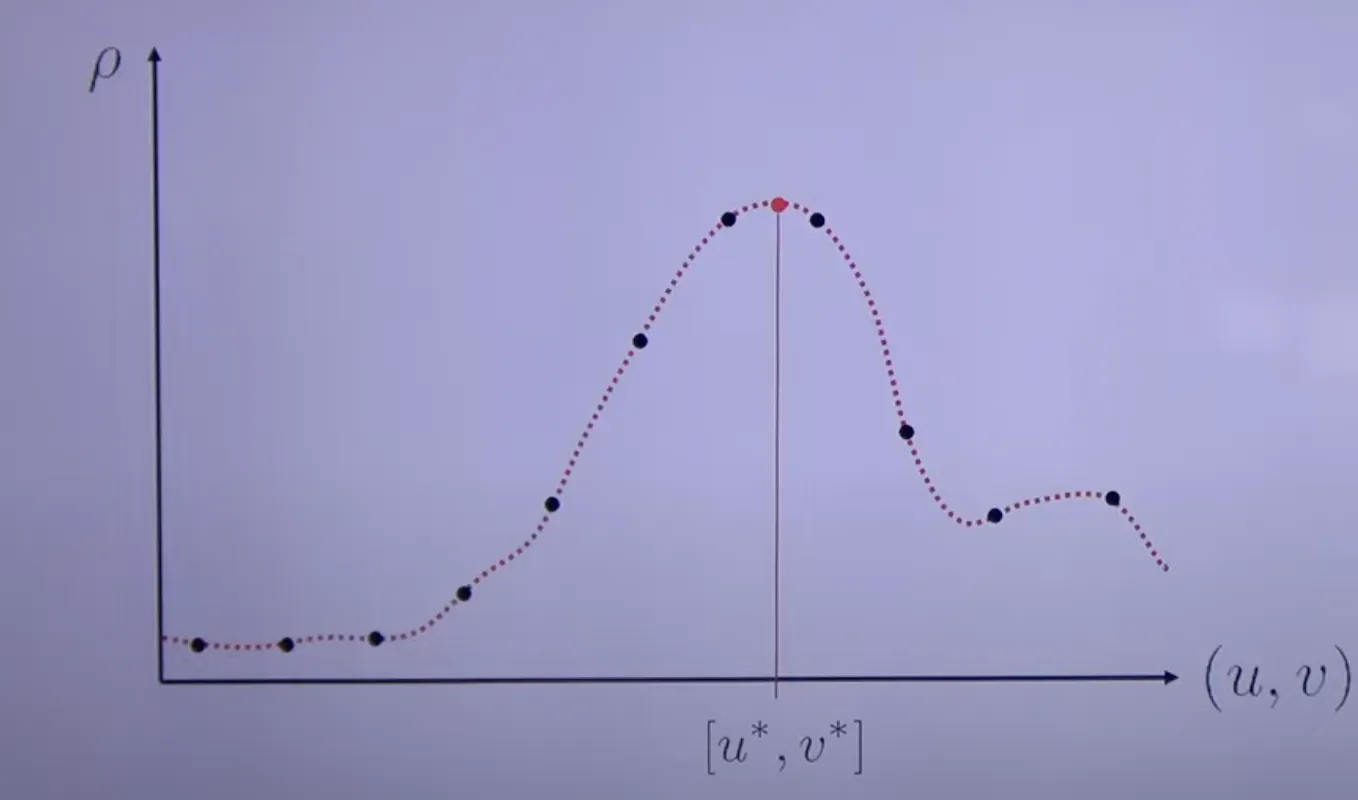
Subpixel Estimation for CC
CC에 의한 매칭 결과는 정수에 기반하므로 subpixel 방법 사용 시 더 정확하다
검은점 : CC 이산분포, 빨간점 : Subpixel 이용한 연속분포
위의 그래프에서 알 수 있듯이 좀 더 correlation이 높은 값을 알 수가 있다
1.
먼저 기존 CC 연산 방법을 통해 maximum값이 있을 거라고 추정되는 위치를 얻음
2.
그 다음 해당 좌표 근처에서 local maximum을 subpixel 이용해서 찾기
Quadratic Func_이차함수
x : NCC통해 얻은 offset, x* : 우리가 얻으려는 값, A는 2x2 Hessian Matrix, a : 1d 변수
•
미분하기
→
p_i, p_j 는 Sobel operator, Hessian 성분들을 이차 미분을 위한 operator