Search
✅

Classification

링크
Category
Vision Study
Keywords
Classification
KNN
DT
상위 개념
하위 개념
속성
Subcategory
개념 정리
날짜
•
example
◦
Features : pixel intensity value - RGB 값
◦
Classes : {vegetation, no vegetation}
•
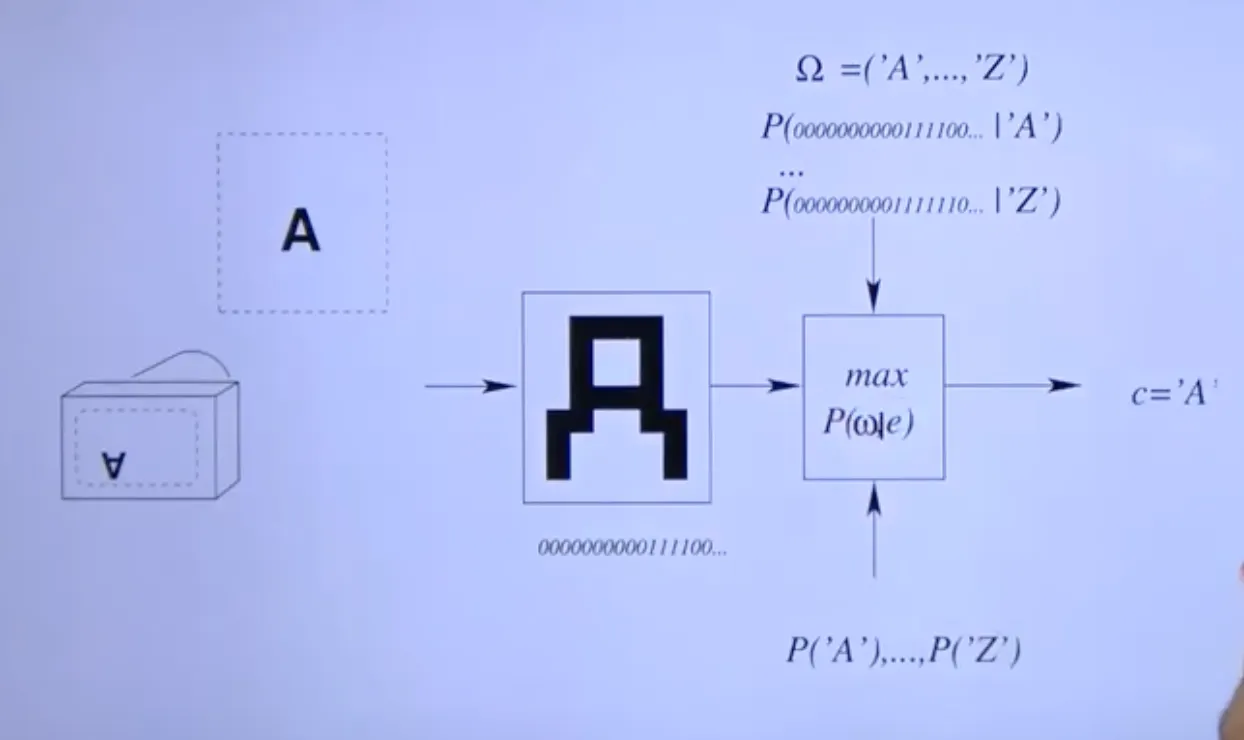
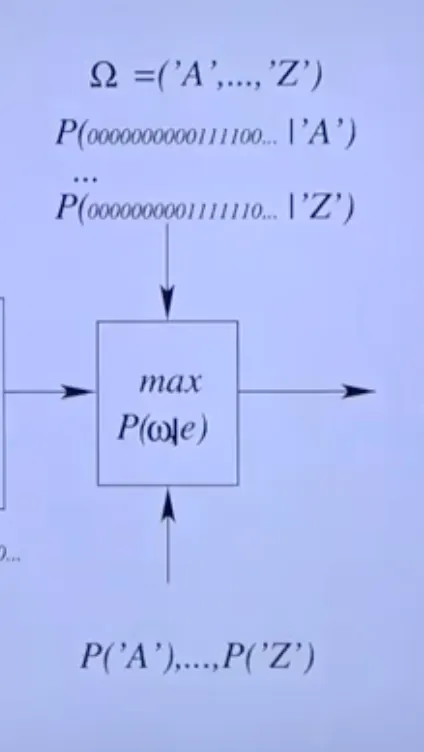
OCR example
오른쪽의 과정이 function ff이고 이는 여러 정보를 통해 train된다.
Training data는 feature vector와 class의 pair.
(e,w)I=1N{(e,w)}^N_{I=1} → learning ff
•
Classification
output : Class label
goal : find a separation of the input that correspond to the classes
•
Regression
output : continuous variable
goal : function that fits a set of data points
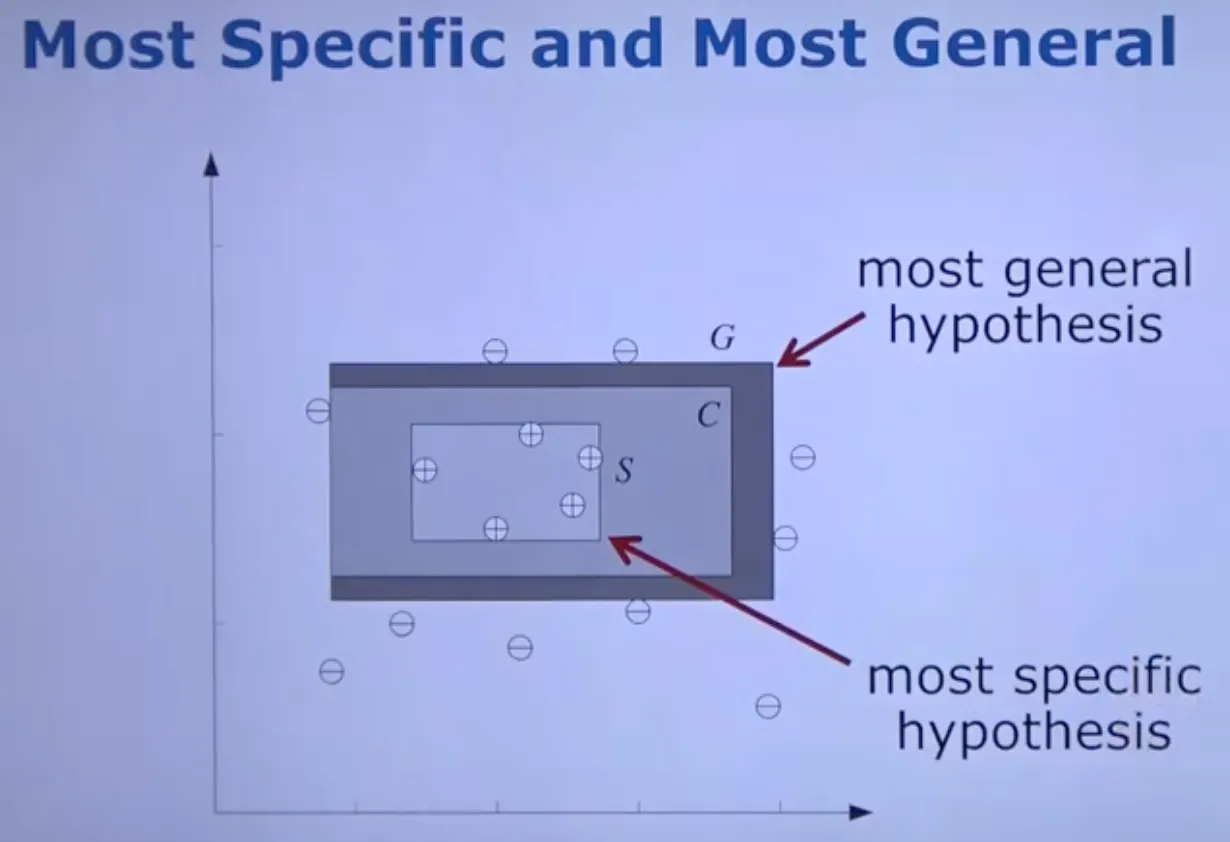
Margin이 최대가 되는 Hypothesis를 골라야 함

Classification Errors

•
False negative : FN
◦
Positive인데 classify 실패
•
False positive : FP
◦
Negative인데 positive로 classify
•
True positive : TP
◦
Positive 옳게 classify
•
True negative : TN
◦
Negative 옳게 classify
FPrate=FPFP+TNFP rate = \frac{FP}{FP + TN}
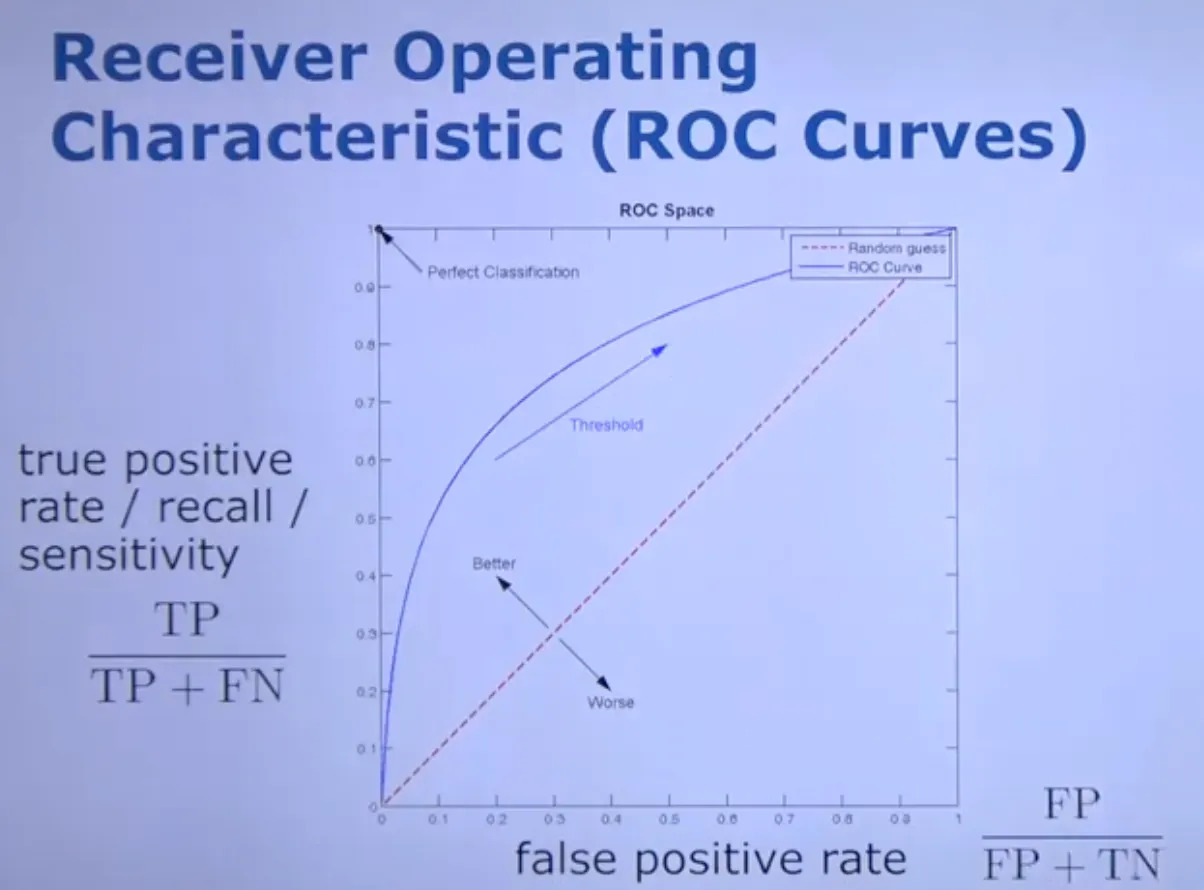
Recall=TPTP+FNRecall = \frac{TP}{TP + FN}, → TP rate
•
ROC Curves
좌상단에 가까울수록 성능이 좋음
•
분류기 평가 지표
◦
F-Score
◦
F1 Score
F1=2∗presicion∗recallprecision+recallF_1 = \frac{2*presicion*recall}{precision + recall}
Precision와 Recall의 조화평균
분류 클래스 간 데이터에 불균형이 이는 경우에 사용

Traditional Classification

•
Testing on different datasets
◦
Extract features
◦
Determine class based the classifier
◦
Evaluate the performance
•
Training
◦
Collecting labeled training data
◦
Selecting and computing appropriate features
◦
Learning the distribution of features for each class or the discriminant function

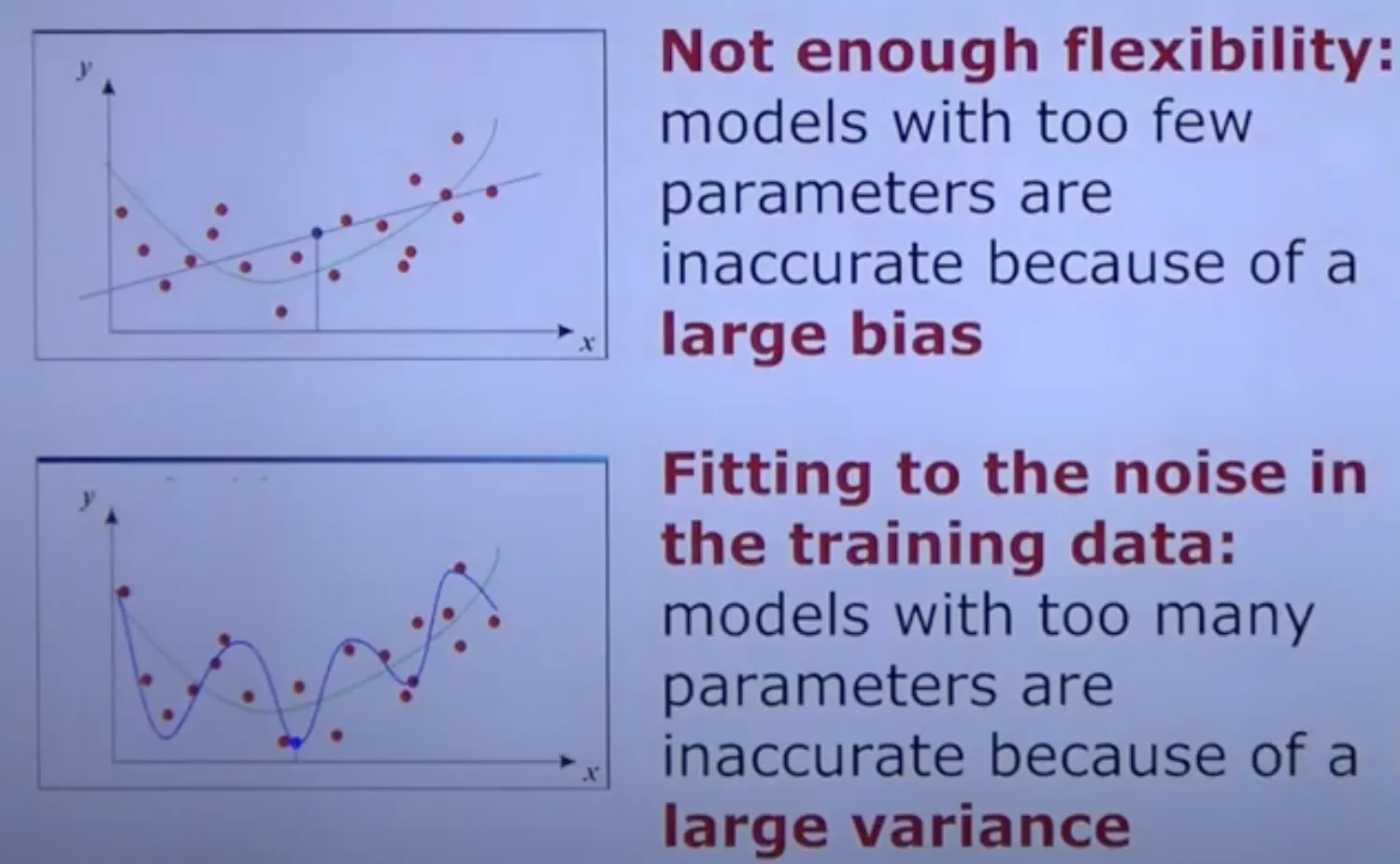
Bias-Variance Trade off

Large Bias :
Flexible하지 않음, Underfitting
Large Variance :
noise에 너무 fit함, Overfitting
E(MSE)=noise2+bias2+varianceE(MSE) = noise^2 + bias^2 + variance

5x2 Cross Validation

Dataset를 2개의 동일한 크기로 나눈다
하나는 training용 하나는 testing용(validation)
두 세트를 swap하고 5번 반복

Nearest Neighbor Approach to Classification

•
Feature 분포는 data에 의해 정해짐
•
Class는 가장 가까운 feature에 의해 할당됨.

K-NN

•
Robustified variant of NN
•
Small K : less robust to noise
•
Large K : consider far away neighbor

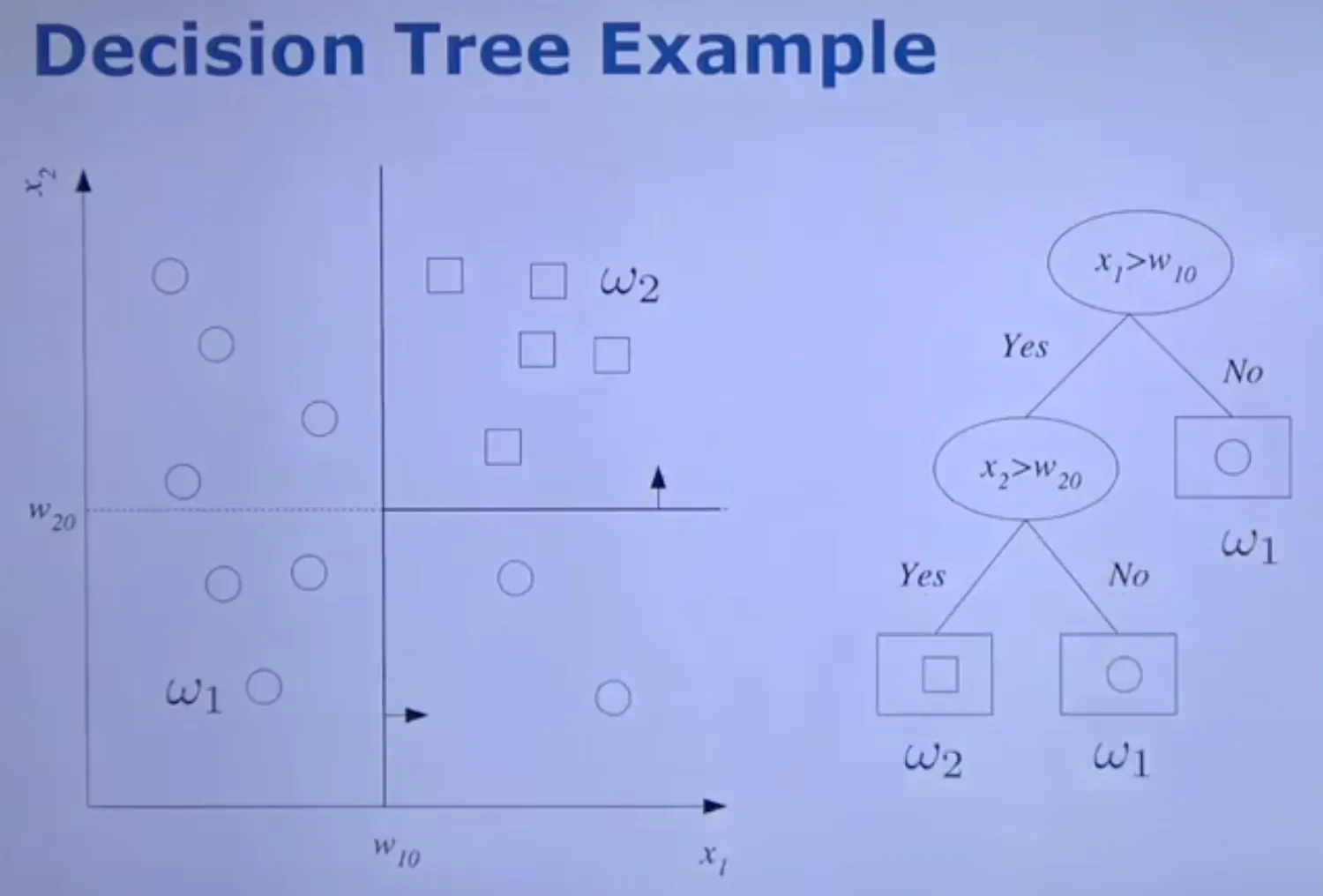
Decision Tree

•
Sequence of Splits of the input space define regions that correspond to classes
•
Hierarchical data structure
•
Setup the tree through training
•
Nonparametric method for classification, regression
1.
root node에서 시작
2.
leaf node면 class label 반환
3.
test func하고 알맞은 branch로 이동
4.
2번부터 다시 반복
•
split decision를 나누는 순서를 모델의 복잡성과 성능에 영향을 준다
•
최적의 arrangement는 NP hard를 통해 구한다.
•
무슨 기준으로 다음 Decision node를 만들어야 할까?
data를 가장 잘 분리하는 class로 선정.
there purer the children, the better split
For any pure child branch, we can create a leaf node

Impurity

defined through the uncertainty in the distribution over the class label
Always select the split that impurity를 최소화하는 방향으로
•
Entropy as Impurity
H(ω)=−∑p(wi)ln p(wi)H(\omega) = - \sum {p(w_i) ln ~p(w_i)}
•
언제까지 split?
◦
Overfitting problem : tree가 완벽하게 data를 나눴다고 해도 다른 data에 대해 generalize되진 X
◦
특정 수준의 purity에 도달하면 멈춰